FoxCalculators - Безплатни онлайн калкулатори!

Експоненциалният гниене / растеж е много полезен в математиката. Експоненциалният разлагат се настъпва, когато темпът на растеж е отрицателен. Експоненциален ръст по същия начин се случва, когато темпът на растеж на стойността на математическата функция е пропорционален на текущата стойност на функцията.

Формулата за експоненциална нарастване на променлива x при (положителна или отрицателна) растежна скорост R, като време t продължава в дискретни интервали (т.е. в цяло число 0, 1, 2, 3, ...), е < b> x _{t = x 0 (1 + r) ^{t .}}

където x _{0 е стойността на x в момент 0. Когато R е отрицателна експоненциална гниене, когато R е положителен, това е експоненциален растеж. Например, скоростта на растеж на R = 5% = 0.05, преминаваща от всяка целочислена стойност на времето до следващото цяло число причинява x втори път, за да бъде 1.05 пъти каква е това, което е било в предишното време.}

Например, R = -0.5, графиката ще намалее (разлагането). Всеки път t се увеличава с 1, x <под> t намалява до половината от предишната си стойност.

Когато r = 1, графиката ще бъде растеж. Всеки път t се увеличава с 1, x <под> t се увеличава с коефициент 2.

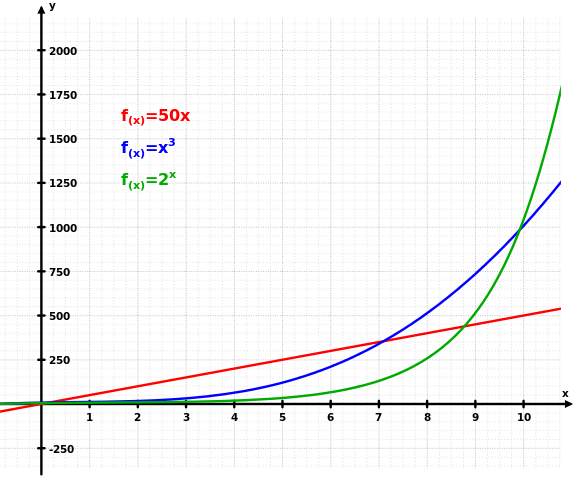
Графиката илюстрира как експоненциалният растеж (зелен) надхвърля и линеен (червен) и кубичен (син) растеж.