FoxCalculators - Безплатни онлайн калкулатори!

В математиката, продължителната фракция е израз, получена чрез итеративен процес на представяне на число като сумата от нейната целоглава част и реципрочната част на друг номер, след което пише този друг номер като сумата от нейната целоглава част и друга реципрочна, така и така На. В крайна продължителна фракция (или прекратяване на непрекъсната фракция) итерацията / рекурсията се прекратява след крайно много стъпки чрез използване на цяло число вместо друга продължителна фракция. Обратно, безкрайна продължителна фракция е безкрайно изразяване. И в двата случая всички цели числа в последователността, различни от първите, трябва да бъдат положителни. Целевите числа AI се наричат ​​коефициенти или условия на продължителната фракция.

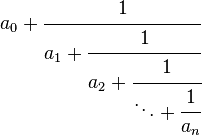
Книтна продължителна фракция, където п е неотрицателно цяло число, _{0 е цяло число, а AI е положително цяло число, за I = 1, ..., n.}

Продължаващата фракция е безкрайна експресия, получена чрез писане на число като сума от нейната целоглава част и реципрочната част на друг номер и отново сумата на цяло число на другия брой и друга реципрочна и т.н. Продължителният калкулатор на фракцията изразява проста фракция като, bo; b1, b2, ..... bn